#模拟
## 题意分析
我们可以先画图,就可以知道在 $n$ 为偶数的情况下,他们永远不会重叠,直接计算 $(k-1)\bmod n+1$。(当 $k=n$ 的情况下,直接计算 $k\bmod n$ 会导致等于 0,因此需要先 $-1$ 再 $+1$)
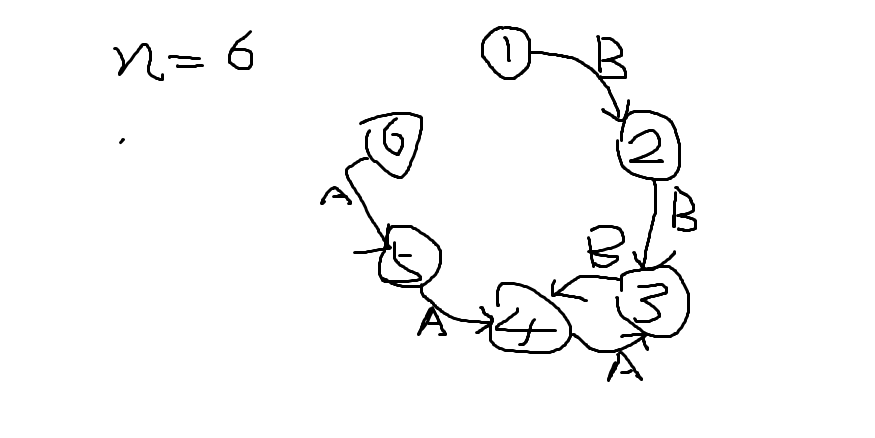
对于 $n$ 为奇数的情况下,我们先计算它在可以重叠的情况下需要移动多少次,再计算挪位置的次数。我们可以发现,在 $n=7$ 的情况下,移动 $3$ 次就需要移位置,那么在 $n$ 的情况下,移动 $\lfloor n\div 2 \rfloor$ 次就需要换一次位置,总共需要换位置的次数是 $(k-1)\div \lfloor n\div 2\rfloor$,按照之前的方式取模即可。
## 代码
```cpp
#include <iostream>
using namespace std;
int t, n, k, p;
int main() {
for (cin >> t; t; --t) {
cin >> n >> k;
if (!(n & 1)) { // 如果不会重叠
p = (k - 1) % n + 1; // 直接计算
} else {
p = ((k - 1) // 原本需要走的次数,这里提前-1
+ ((k - 1) / (n >> 1))) // 需要多走的步数
% n + 1; // 取模
}
cout << p << '\n';
}
return 0;
}
```